√100以上 円 相似の中心 174810-円 相似の中心
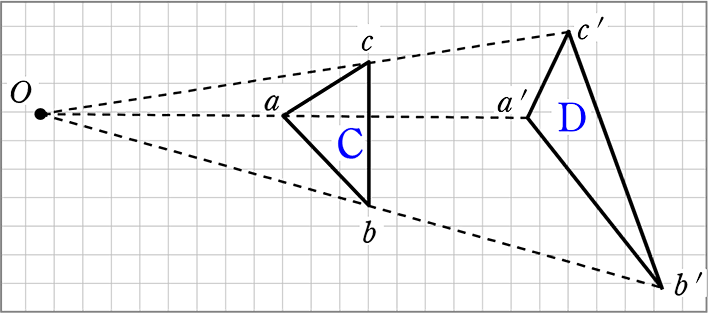
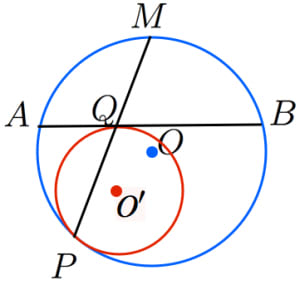
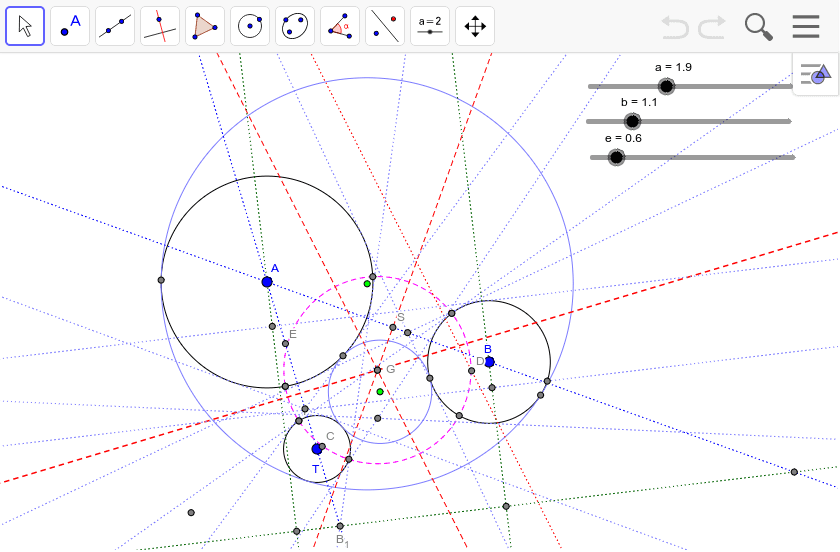
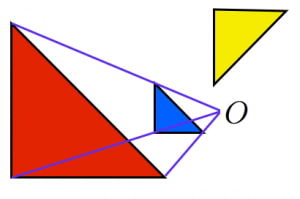
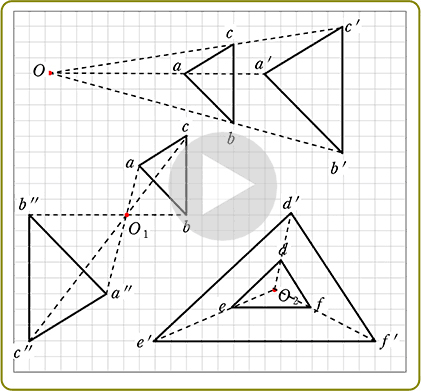
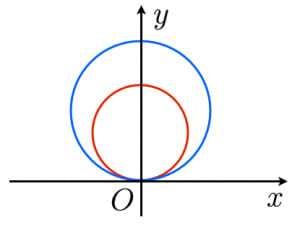
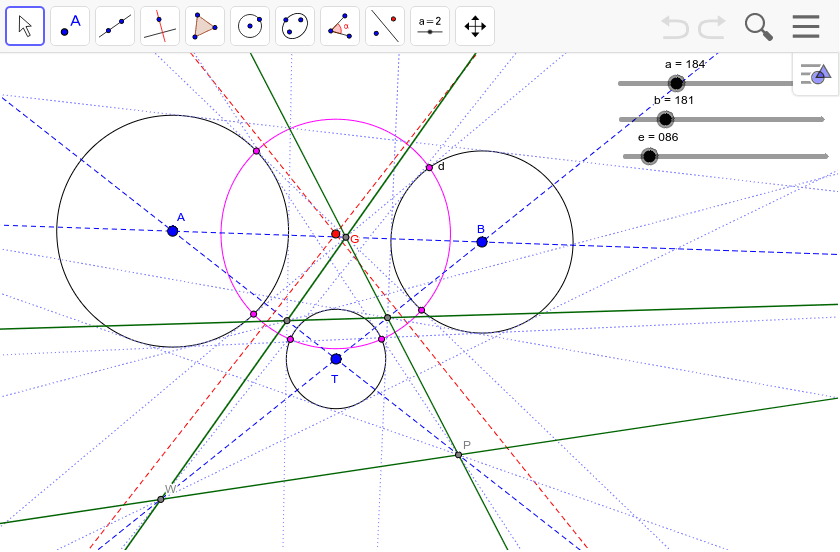
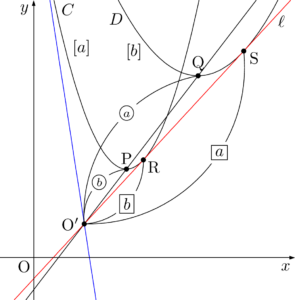
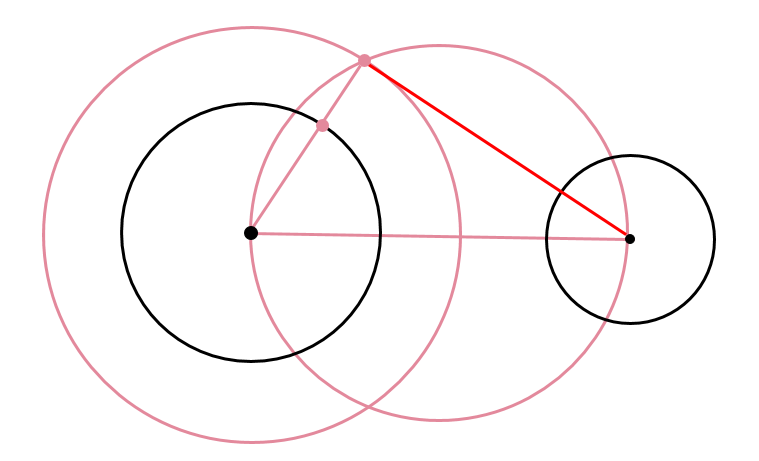
この作図の特殊な例として図3がある。外部にある2つの円の相似の中心 e をとる。e から2つの円に交わる直線を引き、内側の2つを p, q とし、同様に s, t をとる。 この4点は同一円周上にある ため、p と s を通る直線と q と t を通る直線の交点は根軸上にある 。 また、p と q を通るそれぞれの円の
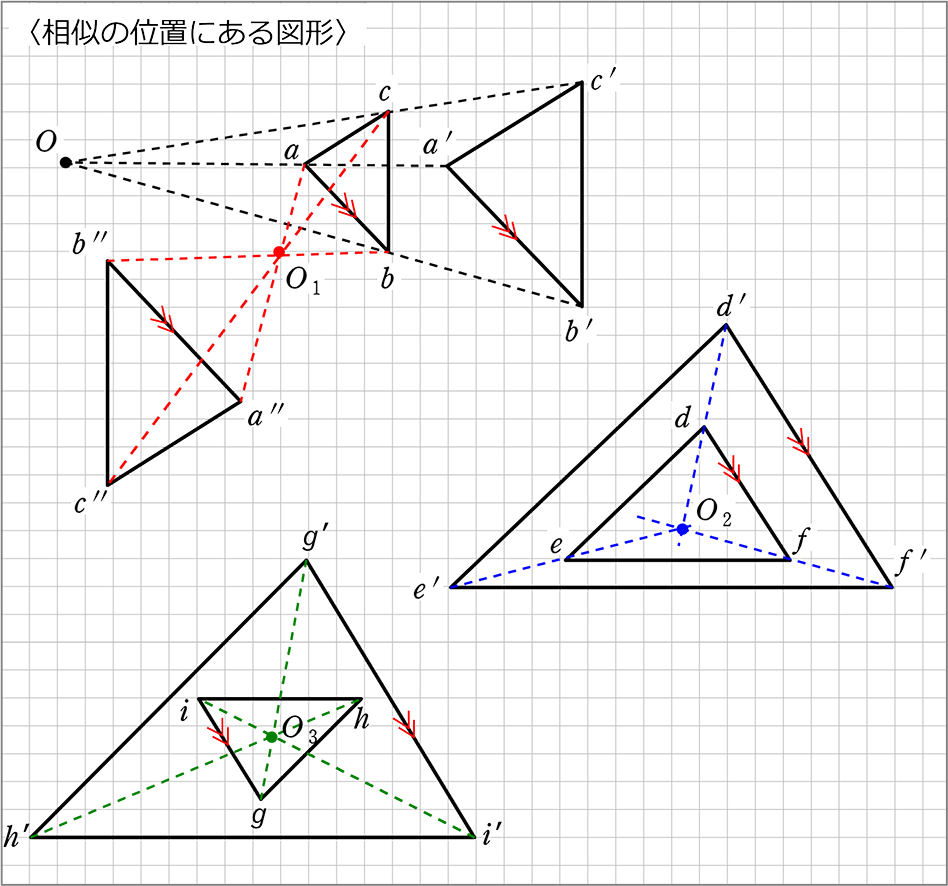
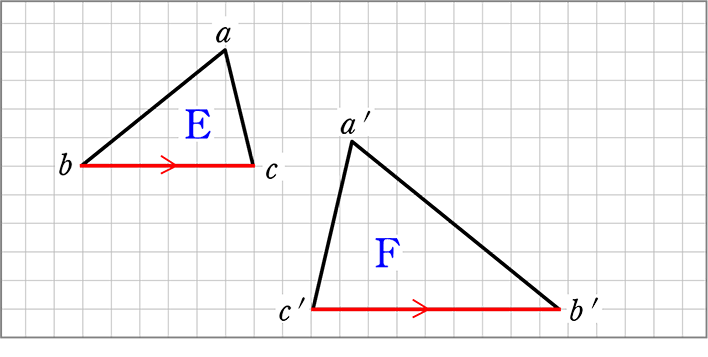
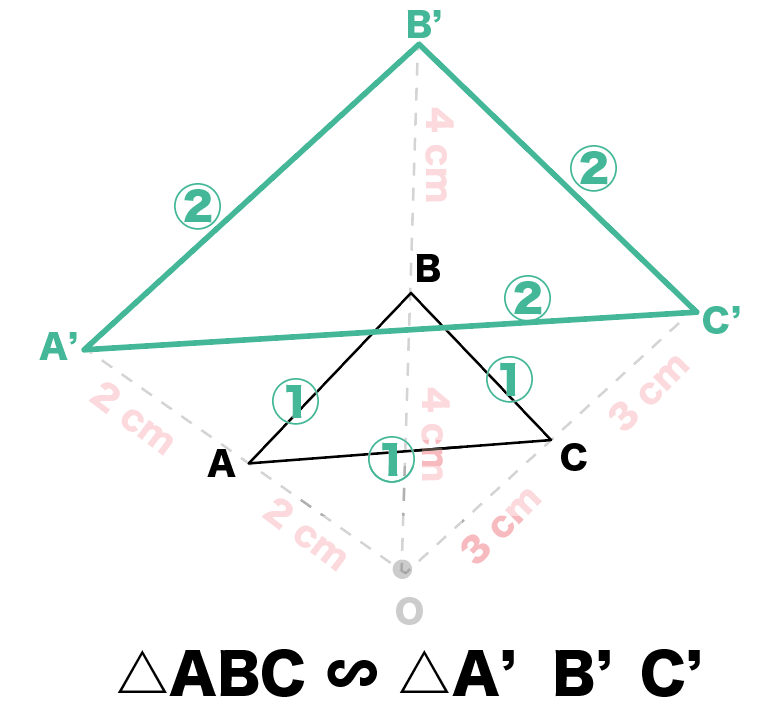
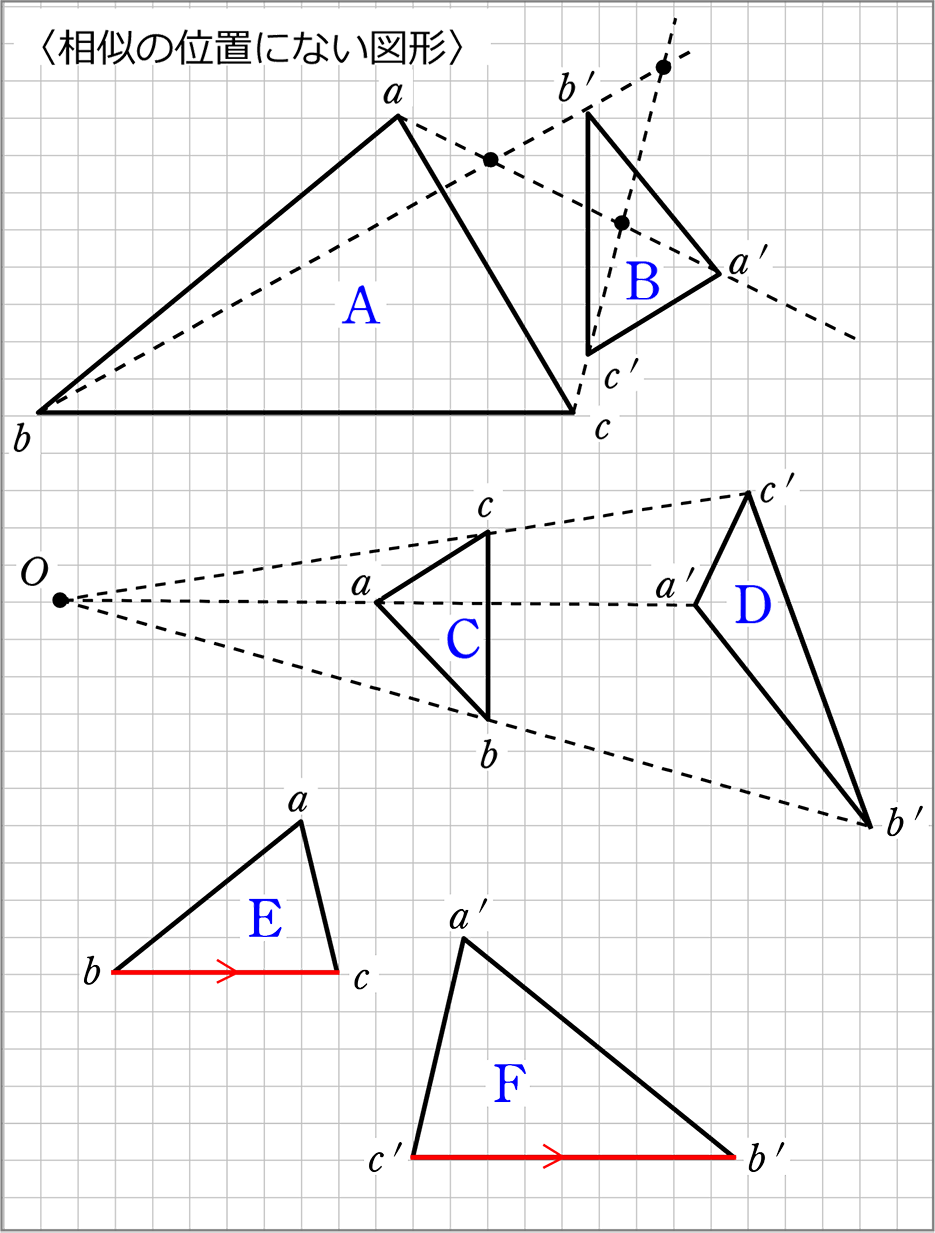
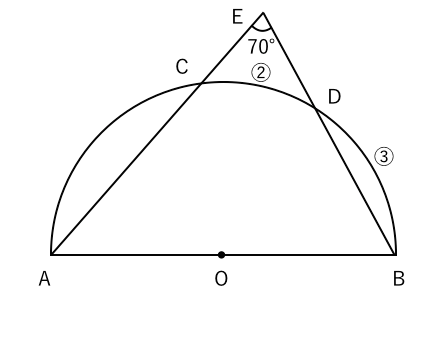
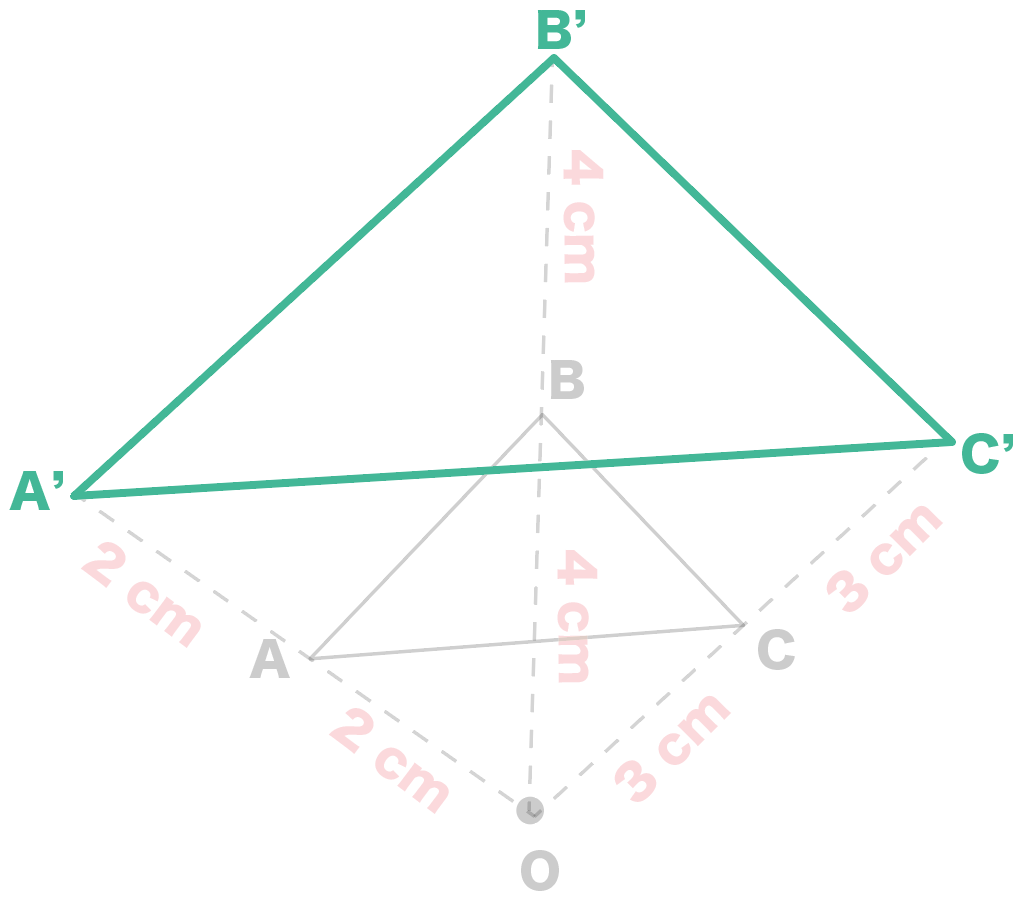
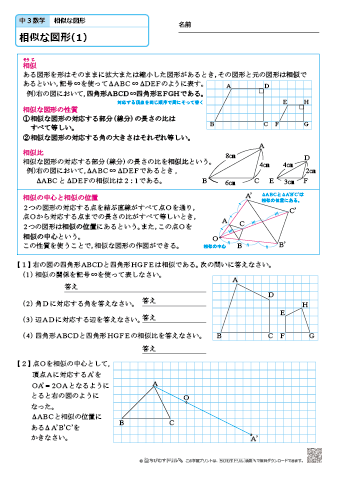
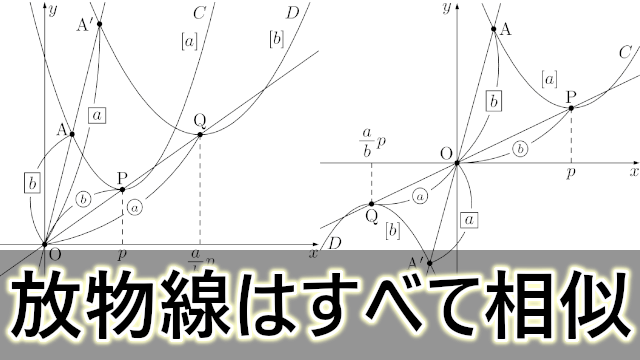
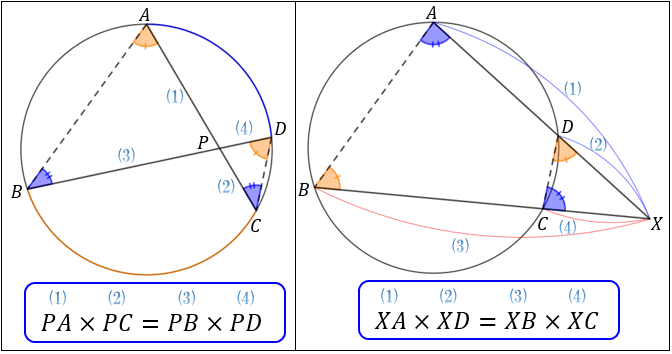
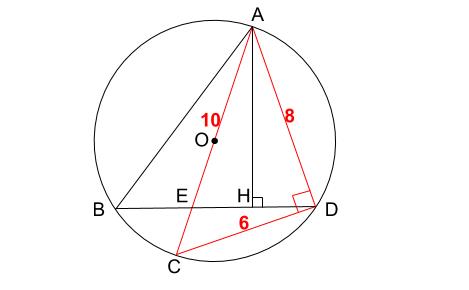
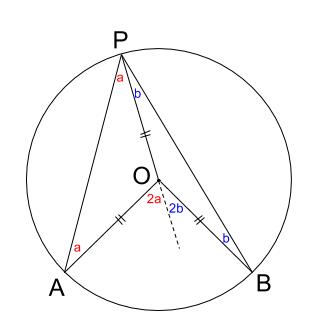
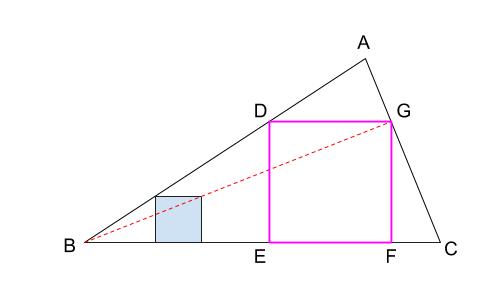
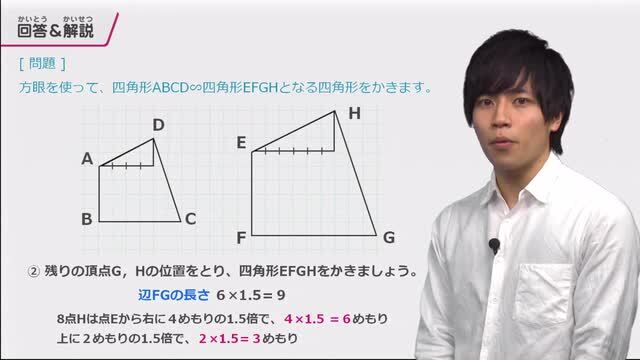
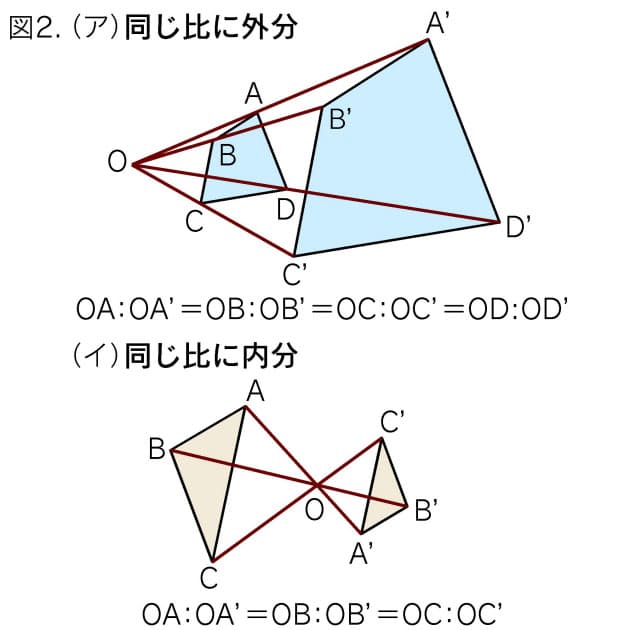
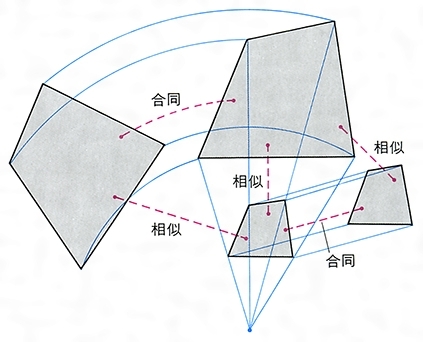
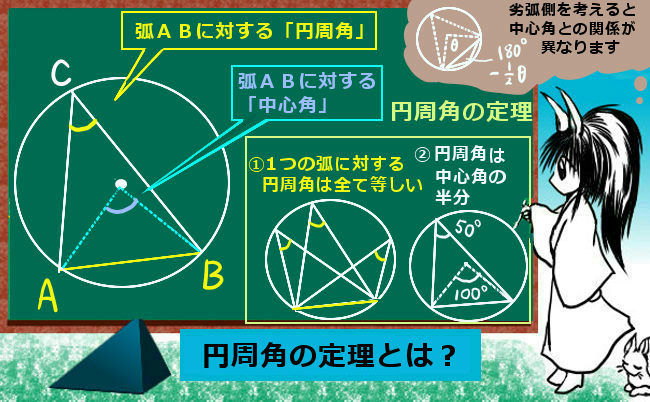
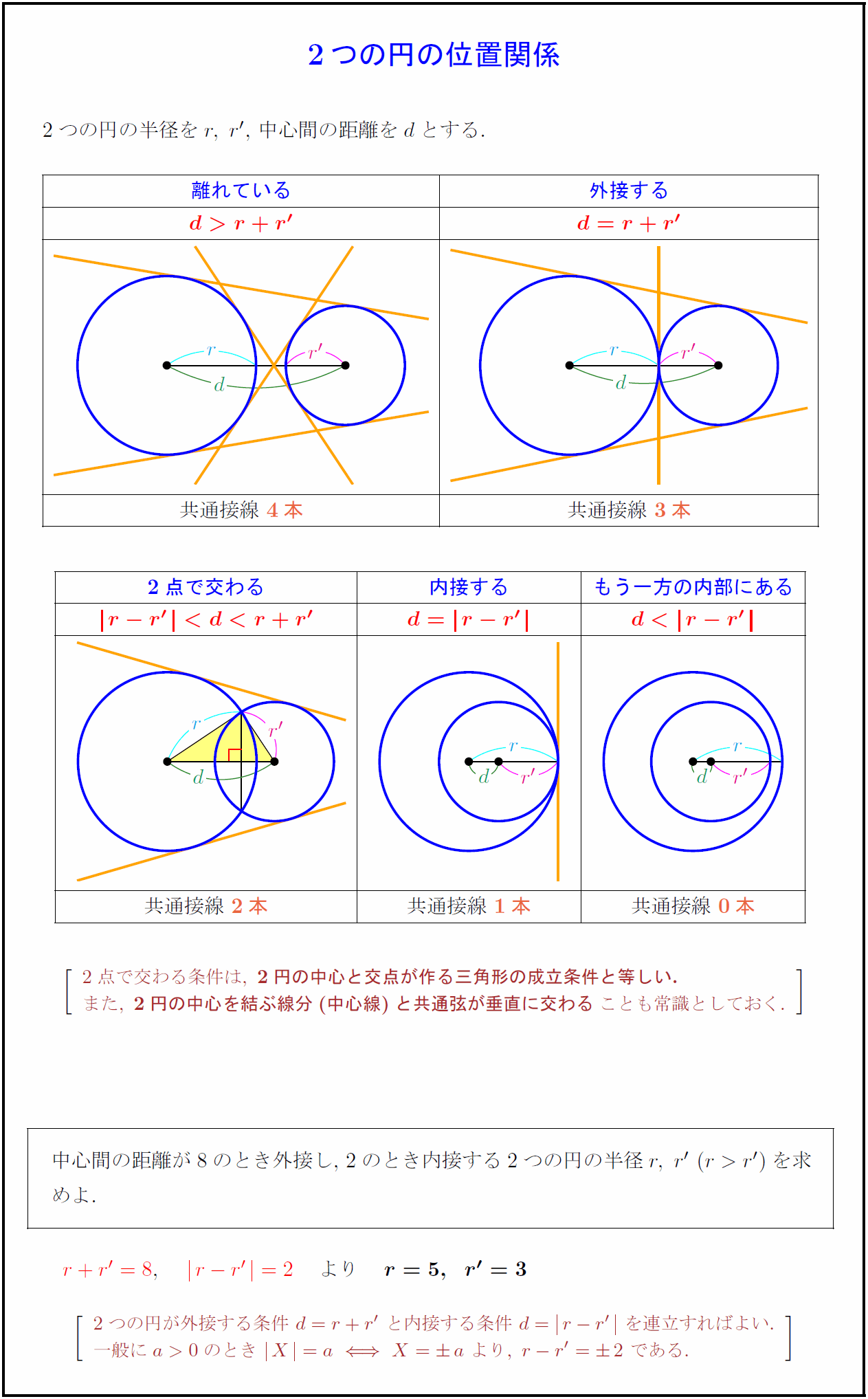
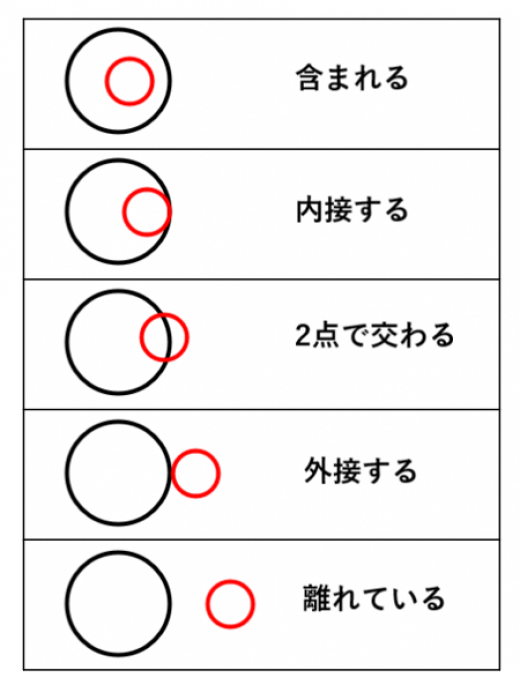
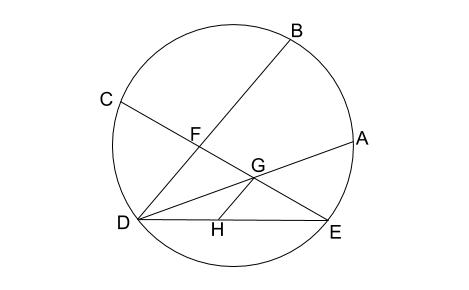
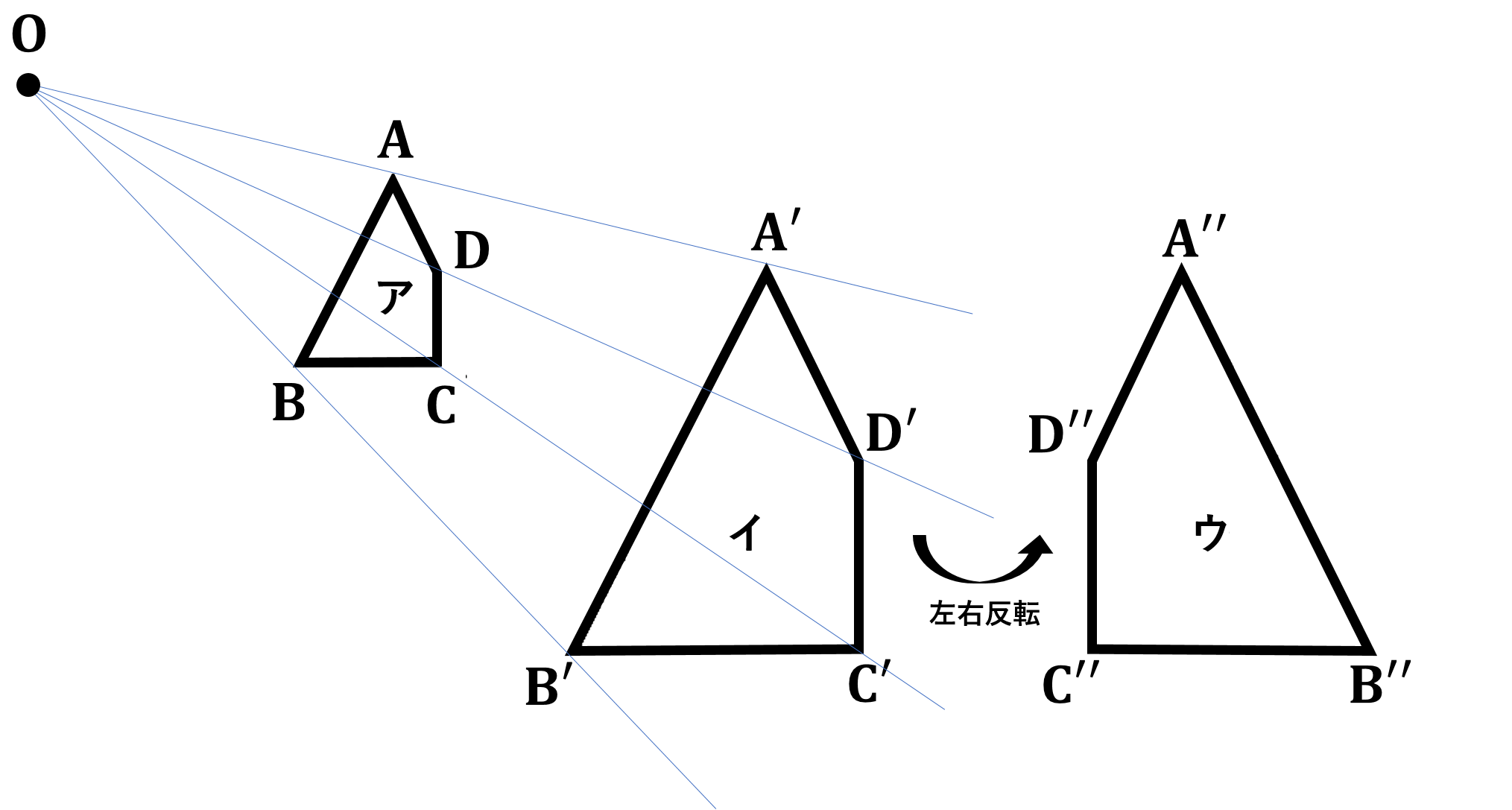
円 相似の中心- 円と相似がからんだ問題も入試ではよく出題されます。 まず、円についての定理のまとめから。 1、円周角の定理(1) なぜそうなるのかの証明は、図に書いてある記号と補助線を参考に自分で考えてみてください。 2、円周角の定理(2)例 相似な図形の例 直線, 正三角形, 直角二等辺三角形, 正方形, 正多角形, 円, 放物線, 直角双曲線, 正多面体, 球など これらはそれぞれ、一方を適当な率で拡大または縮小し、適当に平行移動、回転、鏡映を施すと他方に重なる。 このとき双方は形が同じであるが、大きさと向き(平面上では
円 相似の中心のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
 |  | |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  |  |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 | ||
「円 相似の中心」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
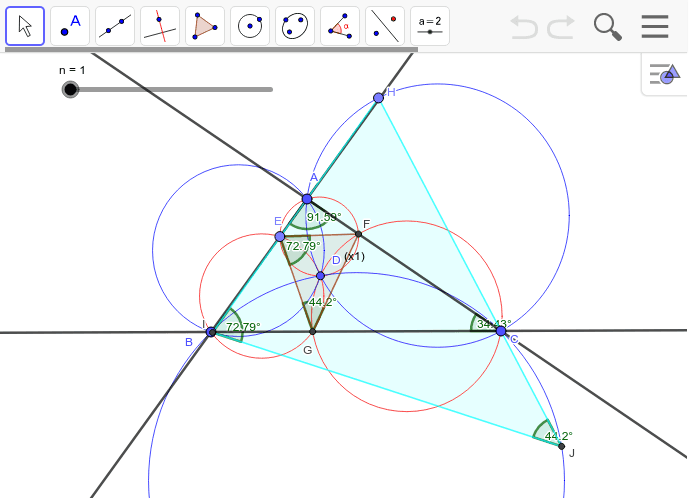 |
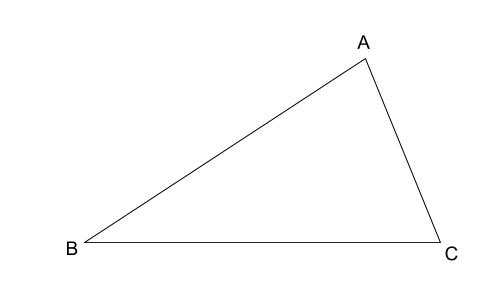
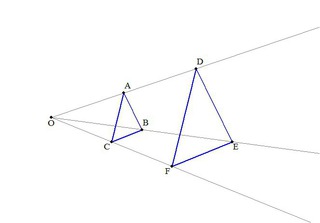
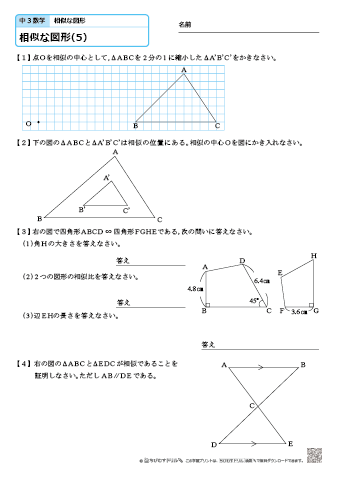
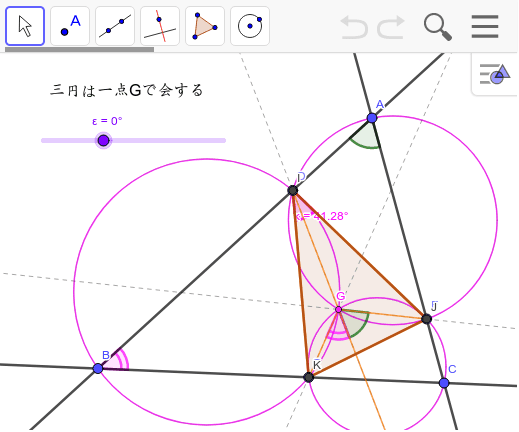
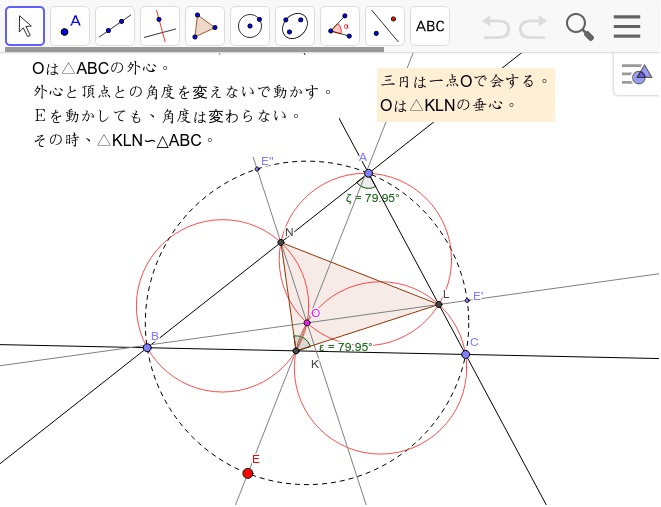
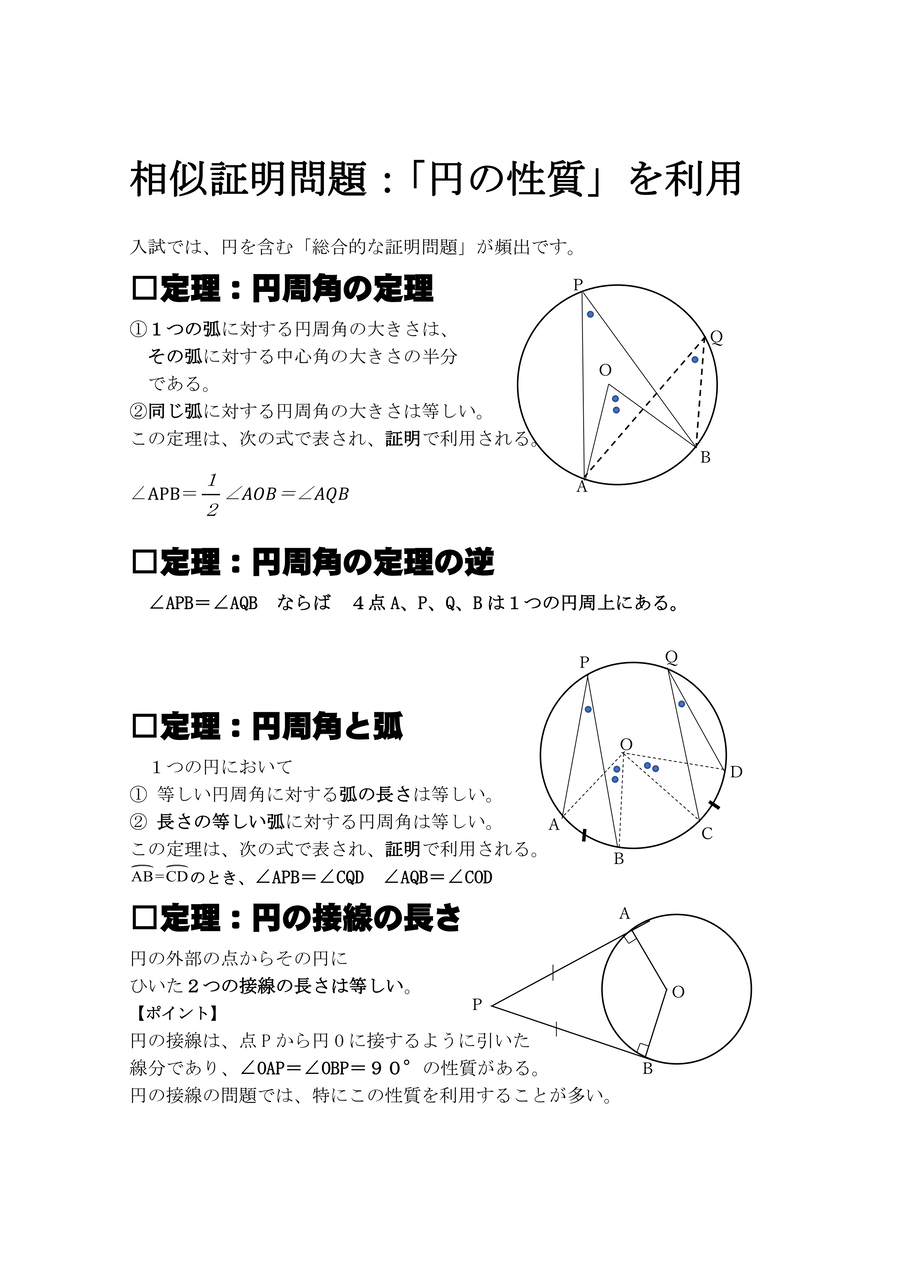
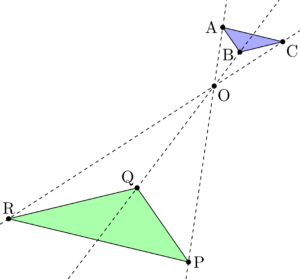
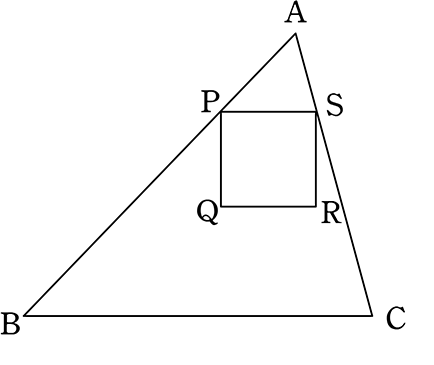
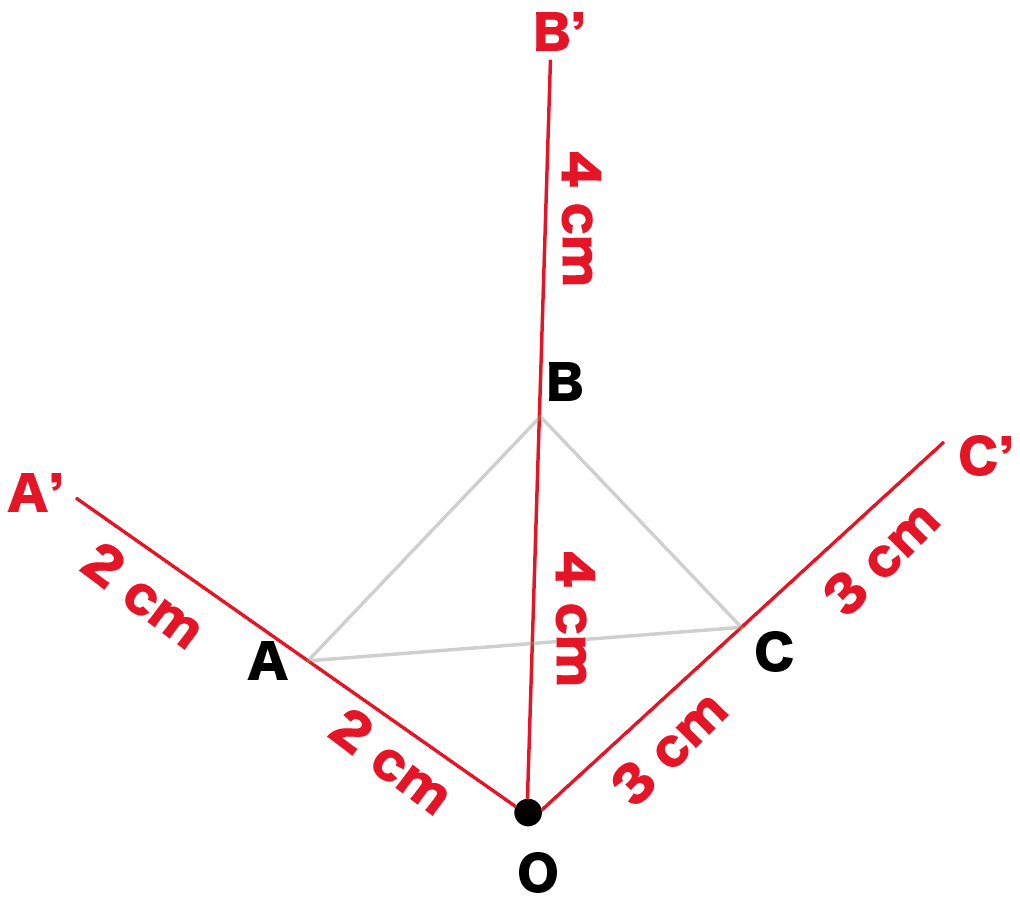
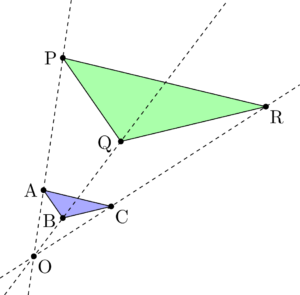
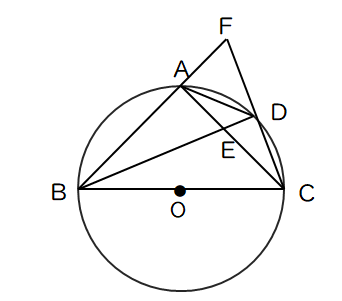
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめはこの作図のためには、頂点を通る3円が一点で会することが重要な意味を持つ。 それらの三角形は全て相似であり、 その相似三角形がどのような三角形になるのかは、 3円が会する点(中心)の位置による。 それを探ってみよう。
Incoming Term: 円 相似の中心, 相似の中心 作図 円,
コメント
コメントを投稿